various existing acceleration techniques for erasure coding, including recent academic work and popular open-source libraries.

Forewords

Erasure coding (EC) strategies essentially provide system-level fault tolerance by encoding k data blocks into m redundant blocks. k can be much larger than m, unlike replicas where m is an integer multiple of k. The obvious advantage of EC is reduced storage space, but more complex data organization strategies introduce additional overhead, such as frequent encoding and decoding operations. Unlike XOR, EC encoding and decoding cannot achieve line speed, therefore, numerous EC acceleration libraries have been developed. Open-source and widely used libraries include Intel's ISA-L, the Jerasure series, and klauspost/reedsolomon in Go. Many companies also have their own proprietary libraries. Moreover, extensive academic research focuses on EC acceleration.

This blog primarily focuses on the end-to-end efficiency of Reed-Solomon (RS) codes, a specific type of systematic code, rather than the mathematical encoding problem itself.

The content was adapted by gemini 2.0 pro from my original notes. If the comments are too harsh, it's not me who wrote them.

Some related background:

• If you are completely unfamiliar with erasure coding, please check drxp's EC blog series for a 101 introduction:
  • Principles: https://blog.openacid.com/storage/ec-1/
  • Implementation: https://blog.openacid.com/storage/ec-2/
  • Optimization: https://blog.openacid.com/storage/ec-3/
• Additional background: High-performance erasure codes - kkblog: https://abcdxyzk.github.io/blog/2018/04/12/isal-erase-1/
  • Parallel lookup table strategy for GF calculations
  • Matrix operation partitioning to improve locality
  • Cauchy encoding matrix: https://abcdxyzk.github.io/blog/2018/04/16/isal-erase-2/

We will first divide the discussion into two categories:

1. XOR-based: Because finite field calculations are not instructions directly executable by the CPU, they are converted into multiple XOR operations.

2. Lookup Table: If the finite field is fixed (e.g., GF(8)), the multiplication results can be stored in a fixed table, and table lookups are used instead of calculations.

XOR-based

DSN '09 TC '13 Efficient Encoding Schedules for XOR-Based Erasure Codes

Jianqiang Luo, Mochan Shrestha, Lihao Xu, and James S. Plank

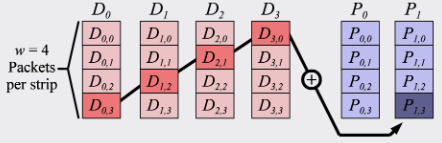
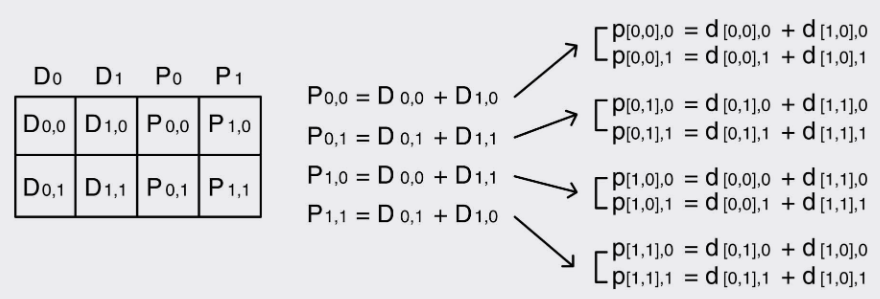
As shown in the figures above, unlike the simple logic of finite field calculations, the computational logic of XOR codes can be understood as splitting each data block into sub-blocks (corresponding to packets). Each sub-parity (sub-p) block requires the XORing of multiple sub-data (sub-d) blocks across rows. Different XOR-code matrices represent different combinational logic. Therefore, much work focuses on proposing more efficient matrices with fewer XOR operations, resulting in less computation and faster speed. This paper focuses on the fact that, while fewer computational operations are important, the caching efficiency of sub-d blocks also plays a significant role, since sub-d blocks are repeatedly accessed during computation.

Therefore, this paper proposes several different scheduling strategies:

• DPG (Data Packets Guided): Performs calculations in the order of packets, processing all calculations related to one packet before moving on to the next.
• DWG (Data Words Guided): Similar to DPG, but iterates by data word.

This improves the locality of sub-d blocks. Because sub-p blocks are not repeatedly read here, pure store operations will only hit the cache. Although this paper targets pure XOR codes like EVENODD and RDP, rather than RS codes, the idea is still quite good.

FAST '19 Fast Erasure Coding for Data Storage: A Comprehensive Study of the Acceleration Techniques

Work by Tianli Zhou and Chao Tian, TAMU.

Open source: https://github.com/zhoutl1106/zerasure This is further work based on Jerasure.

This work is very comprehensive and reading the original paper is recommended; it can be considered a small survey. Zerasure combines and optimizes several existing erasure coding acceleration techniques, including coding matrix design, computational scheduling optimization, general XOR operation reduction, cache management, and vectorization. It then proposes building a cost function based on the number of XOR and memcpy operations. Simulated annealing is used to choose among multiple mutually exclusive strategies, while non-mutually exclusive optimizations are directly overlapped.

• Adjusting the selection still involves various matching scheduling techniques, as they are mutually exclusive.

It is worth noting that this paper presents several viewpoints:

• It considers the costs of memcpy and XOR to be equivalent.
• XOR vectorization is faster than direct GF calculation vectorization (e.g., ISA-L).
• Cache-related S-CO strategies do not offer significant improvements.

  note: This may be because Zerasure itself is not very fast, and the access patterns of XOR codes are inherently not cache-friendly.

Performance improvements:

SC '21 Accelerating XOR-based erasure coding using program optimization techniques

Yuya Uezato, Dwango, Co., Ltd (Parent company of NICONICO, amazing!)

Open source: https://github.com/yuezato/xorslp_ec

But it's a Rust proof-of-concept. It claims a library will be made, but nothing yet. The tools used are not very system-oriented. But this work is quite interesting.

As can be seen earlier, the process of XOR-based EC is actually logically quite simple, somewhat similar to CUDA kernels, but limited by computational resources, memory access resources, etc. So, this work directly abstracts it into SLPs (a concept from the PL field, Straight-Line Programs), and then uses various SLP optimization strategies to optimize the SLP (automated PL strategies):

1. Compressing: Using grammatical compression algorithms to reduce the number of XORs.
2. Fusing: Using the functional program optimization method deforestation to reduce memory access.
   1. This reduces memory access for intermediate variables, but it seems many are done manually.
3. Using the (red-blue) pebble game from program analysis to reduce cache misses.
   1. A formal objective is created, and then heuristically optimized, performing XOR rearrangement.

[It seems that there will still be conflicts among these multiple strategies. How to make trade-offs?]

This strategy is different from ISA-L, which directly accelerates finite field calculations using lookup tables, without converting to XOR.

Results:

• The optimized EC library outperforms ISA-L in RS(10,4) encoding, achieving a throughput of 8.92 GB/s.
• (Xor)RePair reduces XOR operations by approximately 60% on average.
• The combination of XOR fusion and (Xor)RePair reduces memory access by approximately 76% on average.
• The fusing step provides the largest improvement.

ICCD '23 TCAD '24 Cerasure: Fast Acceleration Strategies For XOR-Based Erasure Codes

Tianyang Niu, Min Lyu, Wei Wang, Qiliang Li, Yinlong Xu, ADSL Lab, USTC

Open Source: https://github.com/ADSL-EC/Cerasure

Challenges:

1. The number of 1s in the bit matrices found by existing heuristic algorithms can obviously be further reduced.
2. Creating pointers for reading/writing data leads to high encoding latency.
3. The trade-off between computational efficiency and spatial locality can be further improved by selecting the packet size.
4. Wide-stripe encoding (stripes containing many data/parity blocks) leads to low cache hit rates for commonly used packet sizes.

Corresponding designs:

1. V-search: Searches Vandermonde and Cauchy matrices and greedily reduces the number of 1s in the matrix to find a near-optimal encoding matrix.
   1. The trans version adds an opt-search: iteratively replaces matrix elements in descending order of the number of 1s in the bit matrix, and excludes those that increase the number of 1s or destroy the MDS property.
2. Uses offset reuse to accelerate the construction of read and write pointers (this engineering trick seems to be due to the strong coupling with ISA-L's interface).
3. Finds a trade-off in packet size selection (computational efficiency and cache), using the L1 cache size to calculate an optimal solution.
4. Decompose: For large stripes, the number of data blocks is larger, putting significant pressure on the cache. Therefore, the calculation is separated into multiple sub-encoding tasks, which are merged at the end.
   1. The trans version adds smart decompose, which greedily combines subtasks during decomposition to increase similarity, so that the previous scheduling is more effective.

Experiments were compared with Zerasure and SLPEC, but not with their implemented baseline, ISA-L. It can be more than twice as fast as Zerasure, but Zerasure cannot outperform the default ISA-L.

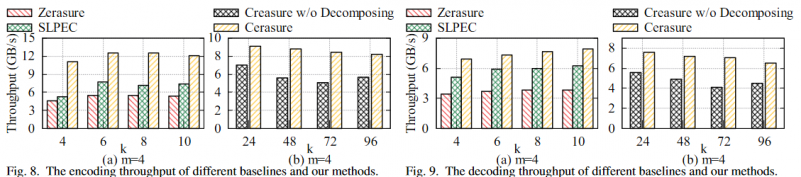
HotStorage'24 Rethinking Erasure-Coding Libraries in the Age of Optimized Machine Learning

Jiyu Hu, Jack Kosaian, K. V. Rashmi, CMU

As mentioned earlier, some have used SLP to automatically optimize XOR organization and scheduling. This paper is even more interesting, directly using TVM to optimize EC computation scheduling. The difference between EC matrix calculations and NN matrix calculations is that the internal subunits are performing bitmatrix XOR.

No internal modifications to TVM are needed, just call the API directly. However, TVM requires this data to be contiguous. They assume that the overhead of memcpy is general for libraries.

But it doesn't feel like it?

This idea is very interesting, but it's quite engineering-heavy to implement. Although it uses TVM, it's not using the GPU; it's still compared with CPU libraries.

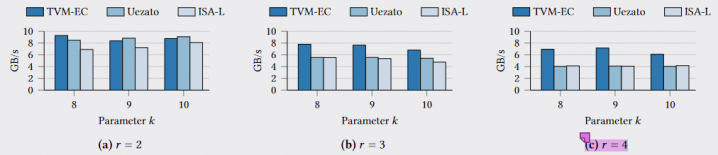
Interestingly, it can be seen that the SC'21 work can no longer outperform ISA-L when r=4. In addition to the hardware issues mentioned in the paper, the main reason is that the increase in XOR operations is not linear for XOR codes with multiple parities. It can be seen that the advantage of TVM-EC increases with a larger number of parities. This may be because the increase in the number of operations provides more optimization space for TVM. Of course, this is an optimal calculation state after learning the parameters, requiring a process similar to preheating.

Introducing this system to existing systems requires a C++ runtime, and the layout needs to be adjusted. In addition, the specific memory access and calculation process becomes opaque, which is actually quite heavy.

By the way, there are also some works that use GPUs for EC:

• ICC'15 PErasure: A parallel Cauchy Reed-Solomon coding library for GPUs
• TPDS'18 G-CRS: GPU Accelerated Cauchy Reed-Solomon Coding
  • Some memory access efficiency optimization and control flow optimization methods are made for GPUs. Because CRS is gf(2), XOR can be used directly.

Lookup Table

Jerasure

http://jerasure.org/jerasure/gf-complete/

Jerasure uses lookup tables for finite field calculations. Including work by James S. Plank such as FAST '13, it is a C library. The precomputed multiplication tables include:

• Log Table: Records the logarithmic value of each non-zero element in the field.
• Exp Table: Records the field element corresponding to each logarithmic value.

It not only supports GF(8) finite field calculations, but also supports finite fields between GF(4) and GF(128). It only has SSE vectorization acceleration.

Different optimization strategies are employed for different values of w:

• GF(2^4): Multiplication of 128-bit data is accomplished through two table lookups using the _mm_shuffle_epi8 instruction.
• GF(2^8): The 8-bit number is split into two 4-bit numbers, each undergoing table lookup, leveraging the _mm_shuffle_epi8 instruction.
• GF(2^16): The 16-bit number is split into four 4-bit numbers, utilizing eight lookup tables and the _mm_shuffle_epi8 instruction. To fully exploit SIMD parallelism, an "Altmap" memory mapping scheme is adopted, mapping a set of every 16 words into two 128-bit variables.
• GF(2^32): Similar to GF(2^16), the 32-bit number is split into eight 4-bit numbers, employing 32 lookup tables and the "Altmap" memory mapping.

A critical problem with Jerasure is its memory access pattern. Here is a pseudo-code example:

void jerasure_matrix_encode(int k, int m, int w, int *matrix, char **data, char **coding, int size) {
    for (i = 0; i < m; i++) { // Iterate through each parity block
        for (j = 0; j < k; j++) { // Iterate through each data block
            if (matrix[i * k + j] != 0) { // If the matrix coefficient is non-zero
                galois_region_multiply(data[j], matrix[i * k + j], size, coding[i], (j > 0));
            }
        }
    }
}

It can be seen that it is centered around parity blocks, which leads to poor locality of data blocks, resulting in poor cache efficiency.

ISA-L

https://github.com/intel/isa-l

Intel's ISA-L may also be for generality (adapting to various platforms and instruction sets). It doesn't have many additional complex optimizations, whether in matrix selection or encoding strategy. It also directly uses lookup tables.

ISA-L also uses split multiplication tables. A complete GF(8) table with 256-byte elements would be 64KB in size, which would put too much pressure on the cache. Therefore, the 8 bits are split into the high 4 bits and the low 4 bits, creating smaller multiplication tables. The calculation also involves two table lookups and one XOR to obtain the final result. The performance advantage of ISA-L comes from relatively simple factors, mainly:

• Extensive assembly unrolling, efficient use of instructions.
• Good memory access locality. After accessing all data blocks in the same row during encoding, all parity blocks are written at once (of course, this is limited by the number of registers; they only support p<=6 in this way, otherwise it needs to be split. But this could be extended).
• Newer instruction set acceleration selection (e.g., AVX512, GFNI).

ISA-L's handwritten assembly here is similar to writing CUDA kernels. Interestingly, many EC implementations, even in top conferences, often use ISA-L's standard encode interface for indirect implementation. However, these self-made interfaces are not very particular about instruction execution efficiency. Writing assembly code in the style of ISA-L would result in at least a one or two times improvement (although this may not be their focus).

FYI, ISA-L also has some minor limitations:

Summary is ISA-L EC can use any encoding matrix, performs the same operation regardless of encoding matrix provided and the documentation is clear about the limitations of gf_gen_rs_matrix(). So not a bug in ISA-L.

Vandermonde matrix example of encoding coefficients where high portion of matrix is identity matrix I and lower portion is constructed as 2^{i*(j-k+1)} i:{0,k-1} j:{k,m-1}. Commonly used method for choosing coefficients in erasure encoding but does not guarantee invertable for every sub matrix. For large pairs of m and k it is possible to find cases where the decode matrix chosen from sources and parity is not invertable. Users may want to adjust for certain pairs m and k. If m and k satisfy one of the following inequalities, no adjustment is required:

• k <= 3
• k = 4, m <= 25
• k = 5, m <= 10
• k <= 21, m-k = 4
• m - k <= 3

GFNI

A new feature introduced in ISA-L v2.31. The distributed interface is ec_encode_data_avx512_gfni. The Go EC library https://github.com/klauspost/reedsolomon also provides a similar interface. The GFNI instruction set directly supports GF multiplication operations at the hardware level, eliminating the need for additional lookup tables, bit operations, etc. On corresponding platforms, my test results show that GFNI+AVX512 can double the performance compared to ordinary AVX512 single-threaded.

锐评

Since our paper is still under review, this section will be expanded upon in the future…