ECWide uses wide stripe to decrease redundancy while avoid repairing bandwidth waste.
erasure code
Erasure code is a low-cost classic method to prevent data loss. The key idea is using extra storage space encoded by some scheme (e.g. RS code…) to re-generate some lost data. You can say RAID5 or RAID6 is a kind of local erasure code.
check here to know more

The rest of this article will assume all readers know some background of EC.
insight
challenge
Normally, EC can provide redundancy $\frac{n}{k}$ (about 1.18~1.5), and use $n-k$ chunks to store parity chunks. It's far smaller than a replication strategy, but if we want to further decrease this number, then wide stripe (e.g. $\frac{n}{k} = \frac{136}{128}$) is a good solution.
However, wide stripe brings other issues:
- Higher repairing cost: you have to collect so many chunks to fix a lost chunk, which will waste cluster bandwidth.
- Encoding also involves many data chunks, so another challenge for computing and network resource!
related work
since the encoding process (generate or update parity chunk) is critical, some researchers focus on accelerating it by locality.
-
Parity locality: to make encoding process can be done in a local node, like locally repairable codes (LRC [2])

-
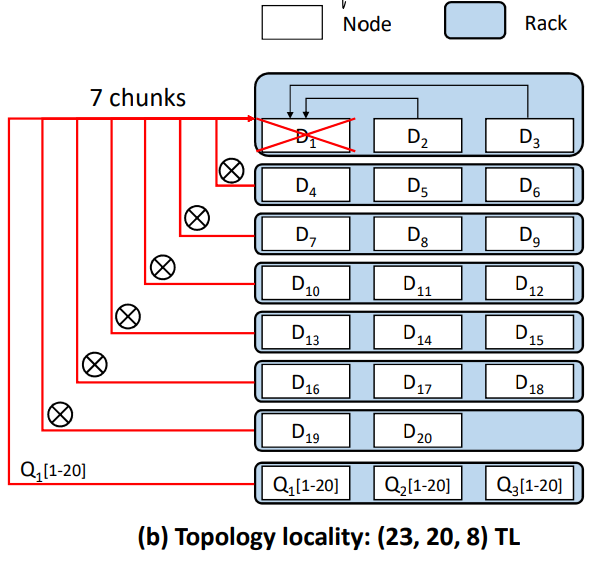
Topology locality: EC clusters are usually in data centers, so there are some network topologies. Transferring data in the same rack is more efficient than transferring them to a data center in another city. So this approach is to minimize cross-rack repairing to optimize encoding.
combined locality
So basically, the two methods both focus on locality. To further utilize locality to accelerate encoding, they produce combined locality, which combines parity locality and topology locality.
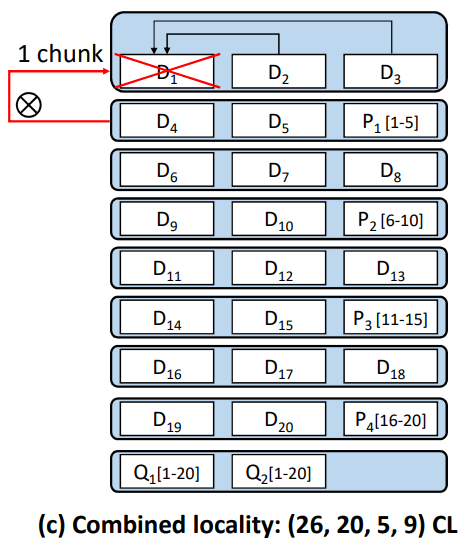
$(n,k,r,z)=(26, 20, 5, 9)$ is an example, showing above.
Combined locality still uses local parity chunks (based on Azure-LRC) but each one for 2 racks. And keep $Q_1[1-20]$, $Q_2[1-20]$ as global parity chunks.
like an Azure-LRC, but placed in a rack style?
a single rack can't place more than $f$ chunks, $c<=f$
repair
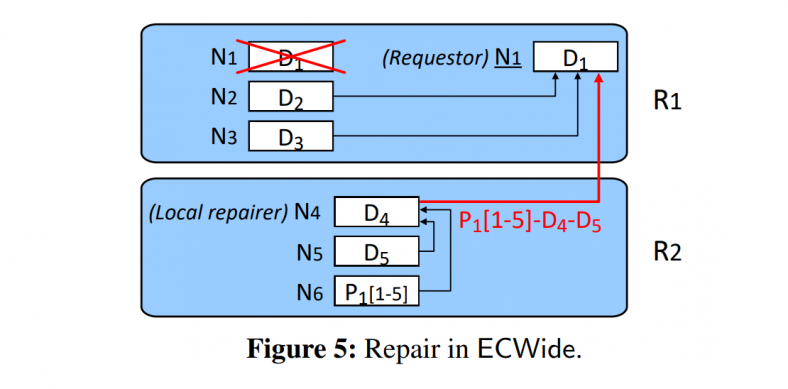
just like LRC, but need extra chunks ($P_1[1-5]-D_4-D_5$) from the local repairer, which contains the local parity chunks.
encoding
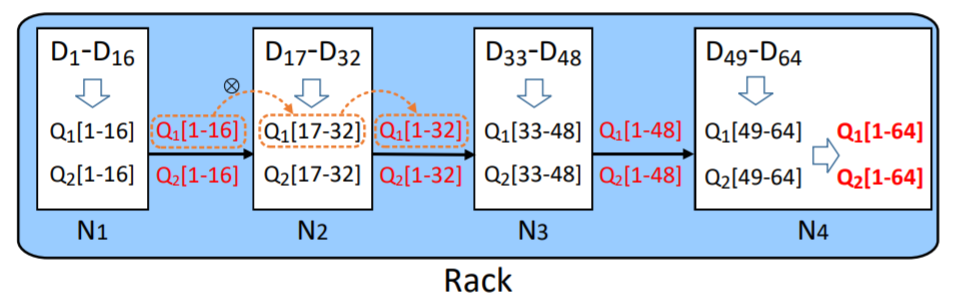
since the encoding process can split into many parts and do it parallelly within a rack, they use a chain-like method. $N_1$ with $D_1$-$D_6$ can generate $Q_1[1-16]$ and $Q_2[1-16]$ and other nodes generate their part.
$D_1$-$D_6$ will be sent to $N_2$ to generate $D_1$-$D_{32}$. And finally $N_4$ can generate $D_1$-$D_{64}$.
why a chain? what about a reversed binary tree? what's the trade-off between transient bandwidth usage and latency?
update
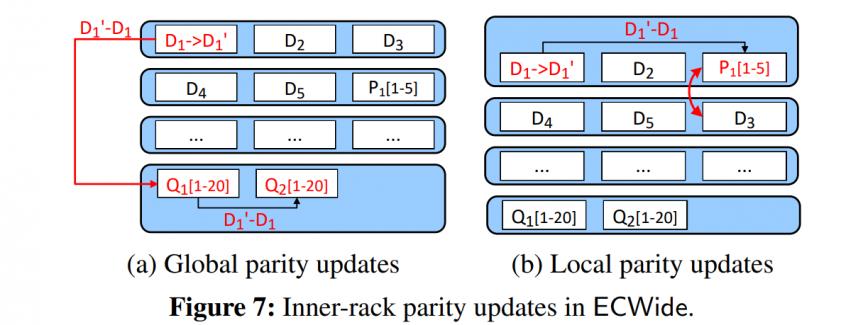
ECWide transfers a delta chunk $D^{'}_1-D_1$ to update global parity chunks. When it comes to updating local parity chunks, it uses a trick that firstly records update frequency, and moves local parity chunks to the hottest rack. This trick can reduce cross-rack transferring.
experiments
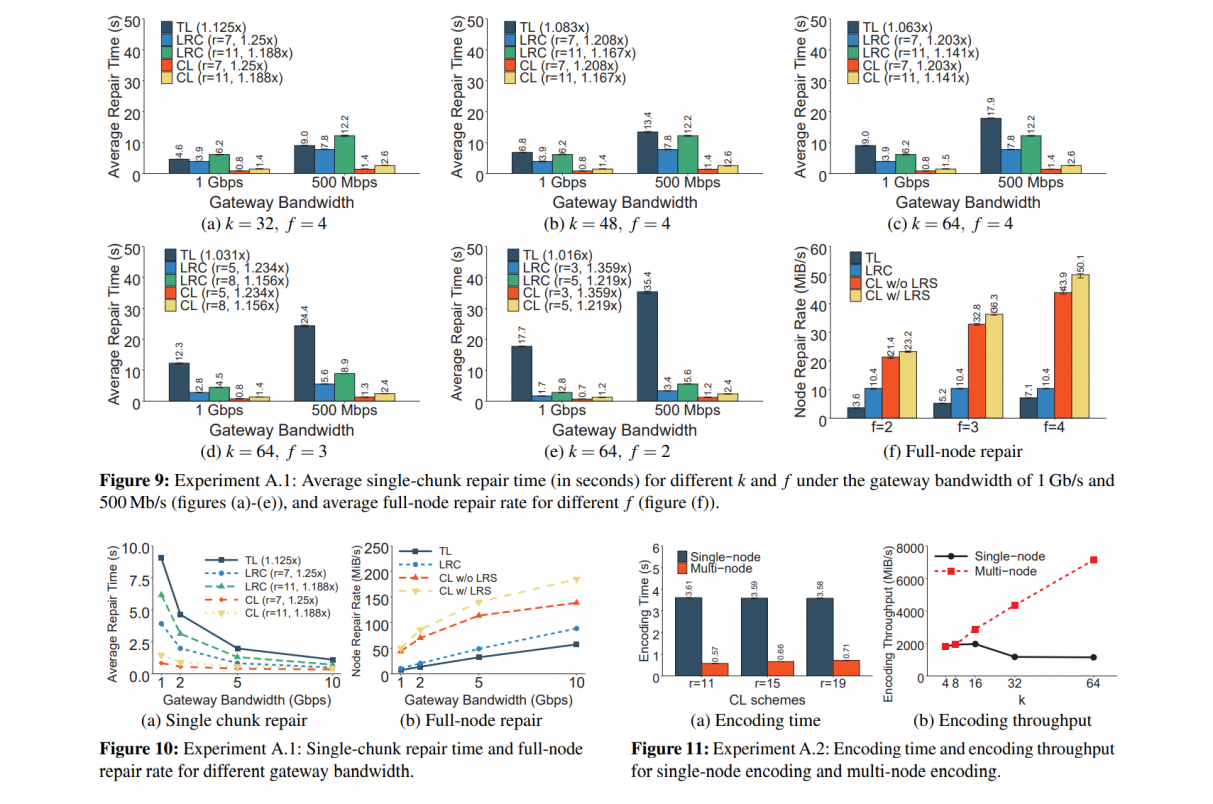
just don't get it why do they split and implement different modules to 2 different platforms…
refer
- Hu, Yuchong, et al. "Exploiting Combined Locality for Wide-Stripe Erasure Coding in Distributed Storage." 19th {USENIX} Conference on File and Storage Technologies ({FAST} 21). 2021.
- Huang, Cheng, et al. "Erasure coding in windows azure storage." 2012 {USENIX} Annual Technical Conference ({USENIX}{ATC} 12). 2012.