序

生成式对抗网络（Generative Adversarial Networks），这是一个多网络对抗的生成模型，它几乎能在所有深度学习需要生成的场景中得到使用（尤其是图形、语音等复杂分布的生成的任务中表现很好）。

这篇文章的主要目的是对这几年基于GAN的各种模型进行一次简单的思路性综述。(〃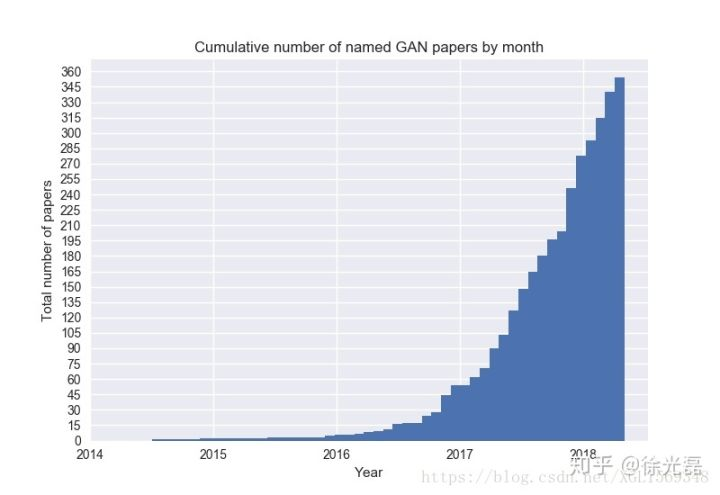’▽’〃) 上图出自GAN Zoo

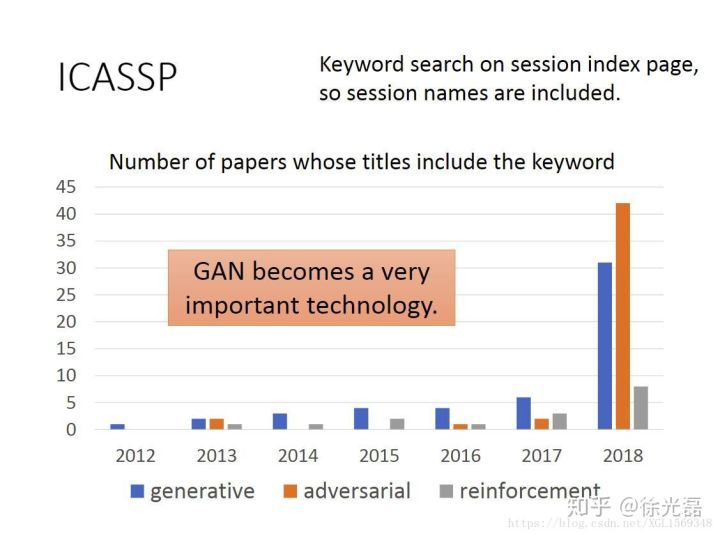
GAN的热度可见一番。本文的主要骨干来自台湾大学李宏毅老师的GAN课程以及论文的阅读记录。

GAN的基础思想

GAN是一类生成模型，和VAE, pixelCNN等生成模型不同的是，GAN引入了NN的对抗环节，来帮助NN生成拟合效果更好的数据。对抗的环节为一个Discriminator NN与一个Generator NN。G的目的为生成拟合效果更好更逼真的数据来骗过D，D的目的为分辨出真实的原始数据和G生成的假数据。如原Paper中打的比方，G是制造假钱的坏人，D是警察专门分辨假钱（“充满暴力与犯罪的例子”）。

原始算法如下：

如上图，在每一次迭代的过程中，对真实数据采样出x，从某个特定分布（如高斯分布）0中采样z。z作为G的输入，得到一批的生成样本。然后先后梯度更新D和G。
下面为对优化目标的分析，$P_{data}(X)$为原数据集的分布，$P_{G}(X, \theta )$为G产生数据的分布。从Maximum Likelihood Estimation开始，G的目标是找到一个最优的$\theta^{*}$有如下式子

$\theta^{*} = \arg\max \limits_{\theta} \prod^{m} \limits_{i=1} P_{G}(X^{i};\theta)$ $= \arg\max \limits_{\theta} \log \prod^{m} \limits_{i=1} P_{G}(X^{i};\theta)$ $= \arg\max \limits_{\theta} \sum^{m} \limits_{i=1} \log P_{G}(X^{i};\theta)$ $= \arg \max \limits_{\theta} E_{x \sim P_{data}}[\log P_{G}(X^{i};\theta)]$ $= \arg \max \limits_{\theta} \begin{equation*} \int P_{data} \log P_{G}(X;\theta) dx \end{equation*} -$ $\begin{equation*} \int P_{data} \log P_{G}(X) dx \end{equation*}$ $= \arg \min \limits_{\theta} KL(P_{data}||P_{G})$

（注意这里的$X^{i}$是从原始数据集中取样的。) 则得到G的目标就是最小化两者的KL散度。

对于D来说，他的目标函数是$V(G,D) = E_{x \sim P_{data}}[\log D(X)] + E_{x \sim P_{G}}[\log(1- D(X))]$。 第一项作为正样本的奖励，第二项作为负样本的惩罚，可以看到这个函数有点类似于Sigmoid的cross entropy。 （PS:其实D用Sigmoid做二分类是不合理的，在$P_{G}$ 和 $P_{data}$的overlap太小的时候，D可以很好的区分两类，这两类都在Sigmoid的左右两侧斜率几乎为0的地方，降低训练效率。采用Linear Regression的方式会更优一些。）

继续得到： $V(G,D) = \begin{equation*} \int [P_{data}(x)\log D(x) + P_{G}(x)\log(1-D(x))]dx \end{equation*}$ 理解为给定一个$X$，$D(X)$都能最大化被积分的式子（假定NN能使$D(X)$为任意函数）。对被积分的式子进行求导，使导数为0，容易得到 $D^{*}(x) = \frac{P_{data}(x)}{P_{data}(x)+ P_{G}(x)}$ （显然为最大值点）。代入 $V(G,D)$ ,得到 $\max \limits_{D}V(G,D)=V(G,D^{*})=-2\log2 + \begin{equation*} \int P_{data}(x)\log \frac{P_{data}(x)}{(P_{data}(x)+ P_{G}(x))/2}dx \end{equation*}) +$ $\begin{equation*} \int P_{G}(x)\log \frac{P_{G}(x)}{(P_{data}(x)+ P_{G}(x))/2}dx \end{equation*} = -2 \log 2 + 2JSD(P_{data}||P_{G})$

所以呢，假如我们现在拥有了一个好的D，那么G上的loss就是两个分布之间的的JS散度。 （PS：用JS散度其实也是不好的，在两个分布都没有重叠的时候，散度项的值是定值，没有办法梯度上升）

对于G来说，则有$G^{*} = \arg \min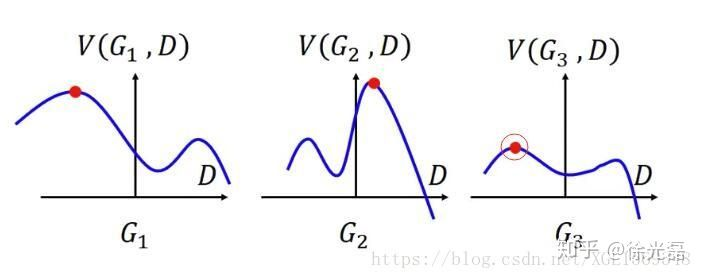 \limits_{G} \max \limits_{D} V(G,D)$ 过程理解为下图：，D随G变化而变化，选择D最大的那点，再在多个G中选择V最低的那点。

训练D与G的时候，其实就是一个D在给G指路的过程，每个迭代过程中，更新多次D，更新一次G（因为G在更新会导致$P_{G}$分布变化，为防止D认不出G，不能更新太多次G，而且在分布变化的过程中，同时丧失了最小化JS散度的意愿）。

同时训练的时候有一些tricks。 按理来说G的目标是$V = E_{x \sim P_{G}}[\log(1- D(X))]$，但是训练时换为$V = E_{x \sim P_{G}}[ - \log D(X)]$，以此提高训练速度。

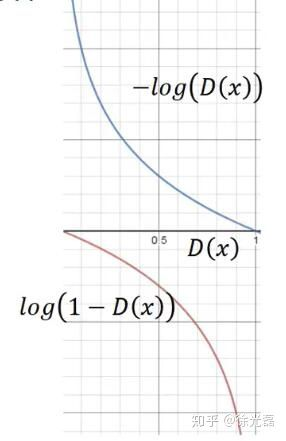
Generative Adversarial Networks

fGAN

在原始GAN中，我们已经证明我们实际上作为loss的是两个分布的JS散度，fGAN提出的是我们可以使用f-散度(f-divergence)这类中的任何散度来衡量。

先解释什么是f-divergence： $D_{f}(P||Q) = \begin{equation*} \int_{x} q(x) f(\frac{p(x)}{q(x)}) dx \end{equation*}$ 如上的公式,P、Q是两个分布，p(x)和q(x)是对x取样的概率。在保证f是一个凸函数，且$f(1)=0$的前提下，我们就获得一个f-divergence。如下，通过修改$f$我们可以获得任意一个f-divergence。

假设$f=x \log x$，代入得到KL-divergence $D_{f}(P||Q) = \begin{equation*} \int_{x} p(x) \log \frac{p(x)}{q(x)} dx \end{equation*}$

同理假设$f = -\log x$，我们就得到Reverse KL，假设$f = (x-1)^2$，我们就得到Chi Square （前文中提到的Least Square其实也可以推出来用的是卡方）。

因为f是一个凸函数，我们先引入共轭函数（Fenchel Conjugate）进行凸优化，共轭函数（针对向量版本）是函数$y^{T}x$和函数f(x)之间差值的上界，同时它自身也是一个凸函数，定义如下 $f^*(y)=\sup_{x \in \mathbf{dom}f}(y^Tx-f(x))$

如下图进行直观理解，y是一个常数，我们要求的差值是两条平行线之间在y轴上的距离

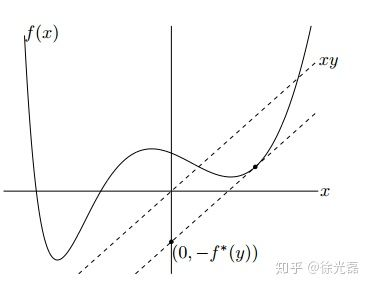
因为共轭的关系是可逆的，我们得到如下式子

t是D输出的scalar，我们写作$D(x)$，得到 $D_{f}(P||Q) \approx \max \limits_{D}$ $\begin{equation*} \int_{x} p(x)D(x)dx \end{equation*}$ $-\begin{equation*} \int_{x} q(x)f^{*}(D(x))dx = \max \limits_{D} (E_{x \sim P_{data}}[D(X)] - E_{x \sim P_{G}}[f^*(D(X))] ) \end{equation*}$

这时候我们就写出了GAN的对抗形式。

更换散度带来的好处包括解决Mode Collapse问题还有类似的Mode Dropping问题。指假如我们的目标domain Y包含三个子domain a\b\c，但是我们的G只能生成a中的样本，虽然这样的情况下也能够使得我们的loss很小（比如人脸生成任务，G一直生成同一个人的脸），但是这样显然不符合GAN的任务需求。

如下图，绿色虚线是对于不同散度评价下对于蓝色分布一个较好的拟合情况。对于KL散度，G倾向生成一个平均一点的分布，导致了模糊的现象，对于Reverse KL散度来说，G就很容易倾向产生Mode Dropping问题。 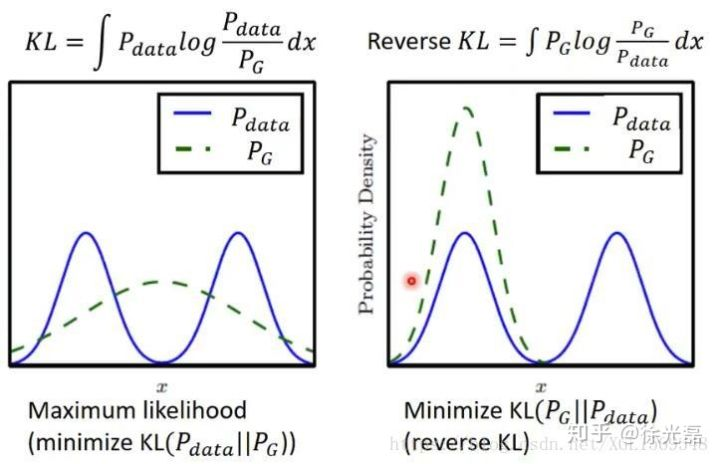f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization

Least Square GAN

Less Square GAN是GAN的一个优化版本。LSGAN解决的问题是，原始D是一个sigmoid二分类器，在D分类效果过好（两个分布解决0或1）的时候，G在跟着D指路优化自身的时候获得的梯度过小，没有办法让两者的分布靠近。在原始的GAN架构中，提出的是减少D训练的次数，防止D分类能力过强，这就对超参的调节提出了很大的要求。

LSGAN将分类的sigmoid输出换成了线性输出，把输出转换成一个回归问题，训练的时候仍然是正样本接近1，负样本接近0。以此优化梯度传递的效果。

Least Squares Generative Adversarial Networks

Wasserstein GAN

在WGAN中，主要的工作是更换了评价两分布接近程度的指标，将JS散度，转换为Wasserstein Distance。 $W(P, Q)=\inf_{\gamma \sim\Pi(P,Q)} \mathbb E_{(x,y) \sim \gamma}[||x-y||]$ （$\gamma$是分布P与分布Q的组合分布，目标为求样本期望距离$||x-y||$的下界）

我们先尝试形象理解一下Wasserstein Distance是什么，假设我们有两个分布P和D，看做是两种土堆，我们要做的是，把P的土堆，挪成像Q的样子（是不是想起来上一篇文章里说过的histogram matching了），我们要记录的就是把所有土挪动的总距离之和。挪土的方法有很多种，Wasserstein Distance就是其中最小的，也就是最近的。

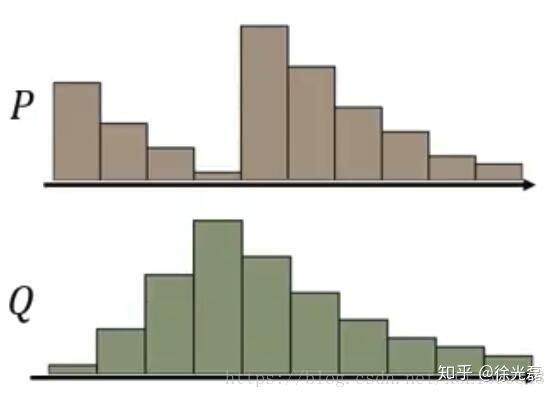
为了求解这个优化规划问题，我们先引入一个Wasserstein Metric帮助理解，这个矩阵就是一个挪土计划表（假装是离散）。这个矩阵的行对应分布Q，列对应分布P。每一行的值代表P里的土被如何分配，每一列的值代表，新土堆里的土由哪些土堆贡献。

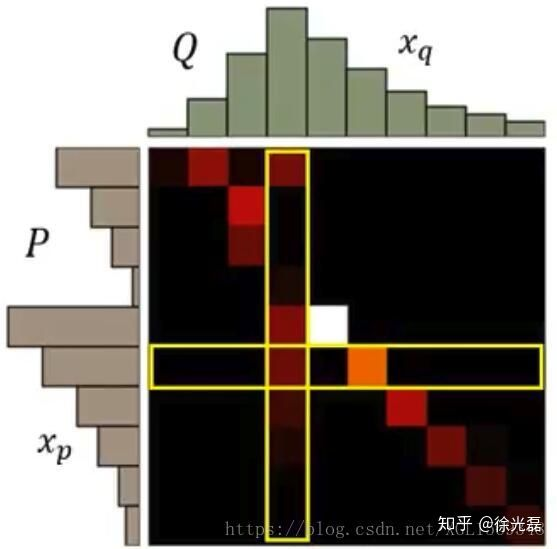
假设$\gamma$是最优的计划矩阵。 那么距离就是 $W (P,Q) = \sum_{x_{P},x_{Q}} \gamma (x_{P},x_{Q})||x_{P}-x_{Q}||$

回到连续的情况下，经过转换后，我们得到的距离如下（别问我怎么转换的，原文说“ the Kantorovich-Rubinstein duality [22] tells us that”。谢谢数学家了）： $W(P,Q) = \sup \limits_{f \in {1-Lipschitz}} (E_{x \sim P}[f(X)] - E_{x \sim Q}[f(X)])$ 所以目标函数成为 $V(G,D) = \max \limits_{D \in {1-Lipschitz}}{E_{x \sim P_{data}}[D(X)] - E_{x \sim P_{G}}[D(X)]}$

（注意这里没有了原来的log，WGAN的D关注指标成为了一个scalar）

1-Lipschitz是符合lipschitz连续条件的一种，这是一个限制函数梯度的条件，一个比通常连续更强的光滑性条件，定义如下 $||f(x_1) - f(x_2)|| \leq K||x_1 - x_2||$ 这里的K常数取1就是1-Lipschitz条件。

原文里并没有追求如何求解保证D符合Lipschitz条件，而是采用了Weight Clipping权重裁剪的方式保证有一定的光滑性。

（再从直观的角度想一下，假如我们在原始GAN模型中，对D训练次数过多，就会导致正负样本被准确分类，D的曲线自然也就成为一个一端很高，一端很低，其他地方都是0的东西，自然也是不满足Lipschitz条件。）

WGAN的距离函数的思路被后来绝大部分GAN模型借鉴，减少了超参调节的压力，解决了由于JS梯度导致的梯度消失问题。 Wasserstein GAN

WGAN-GP

WGAN-GP是WGAN的又一次强化版，在WGAN中，我们使用的Weight Clipping方式并不能帮助我们真正实现1-Lipschitz，甚至说逼近效果也不好。

WGAN-GP提出一个加正则项的方法来逼近1-Lipschitz，理想情况下，我们去对D函数每个地方都求导，拿到一个正则项 $max(0,||\nabla_{x}D(x)-1||)$

但很显然每个地方求导的代价太大，我们就只从$P_{penalty}$这个分布中去采样$x$，完成以下的目标函数

那么现在选择一个合适的$P_{penalty}$成为了一个问题，在原文中，把$P_{penalty}$取做$P_{data}$与$P_{G}$的“中间分布”，从直觉上认为，因为两个分布是互相靠近的，所以要保证的只有$P_{penalty}$分布中的D符合1-Lipschitz（“enforcing it …. seems sufficent and experimentally results in good performence”，翻译过来大概是反正就是work了20190509015633.png）。

训练的时候也做了一些玄学trick，惩罚项被设置为 $E_{x \sim P_{penalty}}(||\nabla_{x}D(x)||-1)^2$ （看上去像是想让斜率逼近1……

Improved Training of Wasserstein GANs

（PS：其实$P_{data}$向$P_{G}$的逼近过程中，显然不一定是走直线的。也就有后续的文章把$P_{penalty}$设置为$P_{data}$，证实结果更好。

（ICLR 2018有一个针对完全符合1-Lipschitz的工作：Spectral Normalization for Generative Adversarial Networks，相关解析见：深度学习中的Lipschitz约束：泛化与生成模型 by 苏剑林

Energy-based GAN

EBGAN把Discriminator修改成了一个Autoencoder，把Discriminator输出的scalar设置为Autoencoder的reconstrcution error（MSE来算距离，这在文中称为能量函数）。基于的假设是如果待评判的图片质量不好，那么重构的结果也不好。

这样做最明显的好处就是，因为训练过程中不再需要负样本，我们不再需要去控制D训练的次数幅度，取而代之的Autoencoder可以提前训练好。

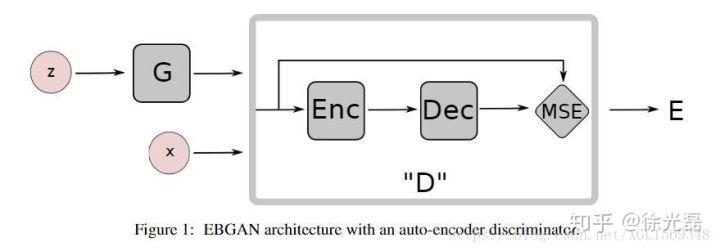
我们使用了来Autoencoder实现D的功能，训练的方式也有改变，因为reconstrcution error是一个难提升，但很容易降低的值，我们要防止对于错误样本的scalar过低导致惩罚过度。我们需要设置一个超参margin， s.t. if $scalar_{neg} \leq margin $ , then $scalar_{neg} = margin$。

EBGAN对$L_{G}$增加了一个正则项repelling regularizer，来保证使用Autoencoder作为D的时候，不会发生mode collapse的情况。

$S \in R^{s \times N}$，代表从encoder output layer取出的一批样本，$f_{PT}(S)$计算这批样本内的平均余弦距离，以此作为惩罚。

Energy-based Generative Adversarial Network

Loss-sensitive GAN

LSGAN的主要贡献是在D输出scalar的前提下，我们想让D学会一个loss。

假设我们拥有多个迭代版本的G，我们希望的是，通过不同代G的生成，D也能区分出不同G的生成与目标分布的接近程度。

Loss-Sensitive Generative Adversarial Networks on Lipschitz Densities

Boundary Equilibrium GAN

前面讲了好几个对原始GAN进行优化的思路，比如WGAN系列，fGAN等等，他们的优化思路集中在于改善衡量分布距离的标准。BEGAN提出了另一个优化的方向，并且提出了一个方法来权衡G的生成质量和生成多样性。

在Discriminator上，BEGAN的目标函数和EBGAN一样，不赘述。

BEGAN的直接目标是优化分布的分布误差之间的相似度，而不是分布的相似度。

$\gamma$是P和Q的任一组合分布，然后用Jensen不等式得出

$m$是分布的期望。

所以我们就可以直接面向优化 $|m_1 - m_2|$ ，虽然距离函数来自于WGAN的思路，但是这可比优化1-Lipschitz条件来得简单不知道多少。我们只需要把其中任意一个推高，另一个推低，就可以满足目标。

文章中提出，我们不需要让模型完全收敛到均衡点，我们设置一个超参$\gamma$，使得 $\gamma = \frac{E(D(G(z)))}{E(D(x))}$

通过调整$\gamma$我们就可以让D在对真实图片自编码和区分图片这两个任务中间进行取舍。

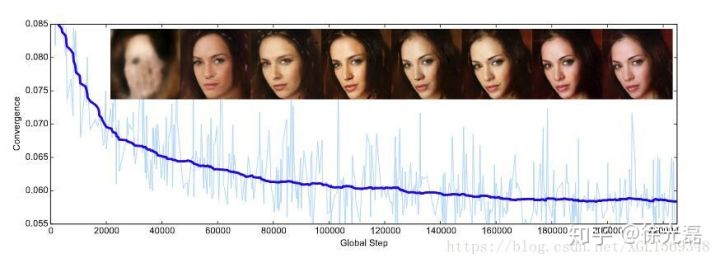
BEGAN的一大优势就是网络结构简单（就是非常单纯地上采样上采样，下采样下采样），降低了训练时对各种trick的需求，什么relu，minibatch，BN全都不需要，而且图像质量被推到了一个很高的水平。

如下图，默秒全了。

BEGAN: Boundary Equilibrium Generative Adversarial Networks

Conditional GAN

CGAN这类 GAN模型主要的想法是为GAN的生成过程中添加一个标签Y有监督地作为输出的一个监督参考。我们使D同时接受G的输出和标签Y两个变量，除了要判断G的输出是否realistic，同时要判断输出与Y 是否有关联 。

目标函数如下 $\min \limits_{G} \max \limits_{D} V(G,D) = E_{x \sim P_{data}}[\log D(X|Y)] + E_{x \sim P_{G}}[\log(1- D(X|Y))]$

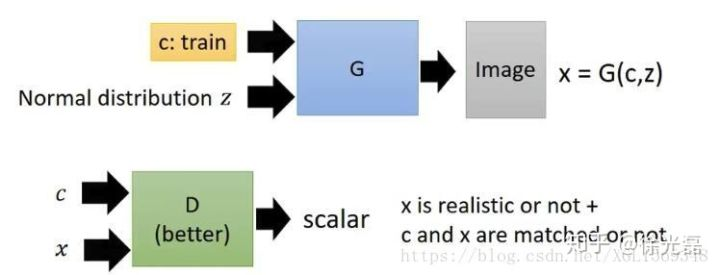
Conditional Generative Adversarial Nets

Cycle GAN

Cycle GAN想要解决的问题是无监督情况下地去实现Conditional GAN的目标。

假如我们一开始的架构和原始GAN类似，首先需要一个$G_{X->Y}$，input图片经过$G_{X->Y}$后生成我们的目标output图片，利用$D$来判别output是否属于原始domain。

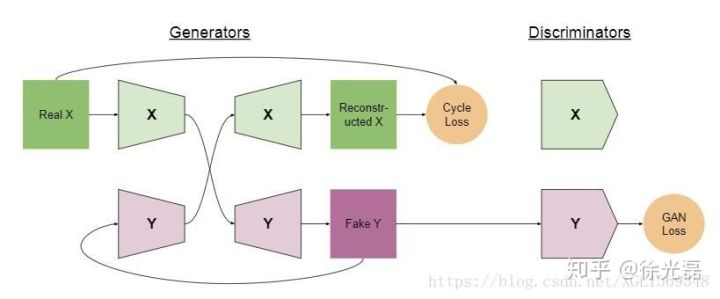
在这样的情况下，$G_{X->Y}$很容易被训练成为一个只会讨好$D$的生成器，而不注重输出的图是否和输入有关（比如不管input是什么，都输出一张目标domain里的原图）。为解决这样的问题，我们引入一个$G_{Y->X}$将output图片重构恢复成一个${input}_2$，在此处引入Cycle Consistency Loss的概念，目的是为了计算${input}$和${input}_2$是否足够接近。

直观上进行理解，假如output生成的图片和${input}$关系不大，那么$G_{Y->X}$就没有能力恢复重构出一个和${input}$非常接近的${input}_2$。

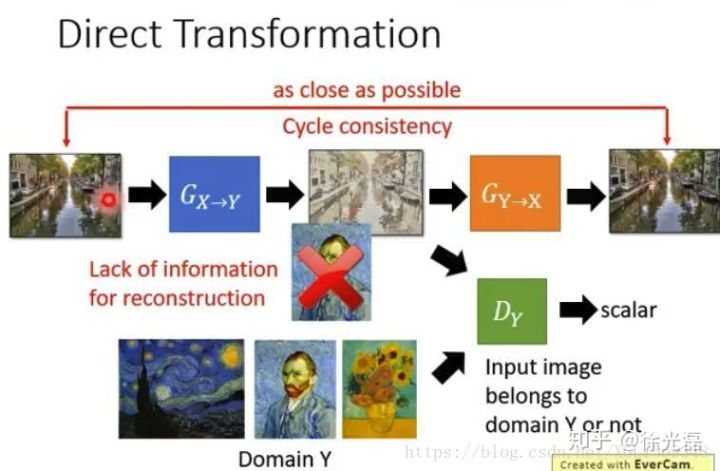
Cycle的做法也可以是走一个双向的路径，既然我们训练了$G_{Y->X}$，那么我们完全可以开一条类似的循环生成路径来把目标domain的图片转化为原始domain的图片（如下图）。

$L_{cyc}(G,F)=E_{x \sim p_{data}(x)}[||F(G(x)-x)||]+E_{y \sim p_{data}(y)}[||G(F(y)-y)||]$ 这里的$G(x)$，$F(y)$分别对应前文的$G_{X->Y}$，$G_{Y->X}$。

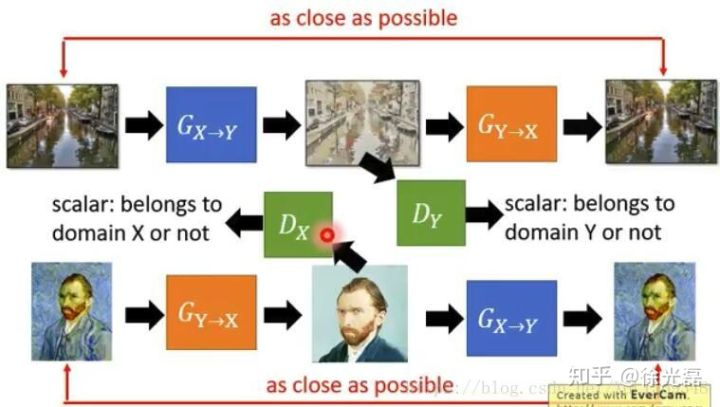
Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks

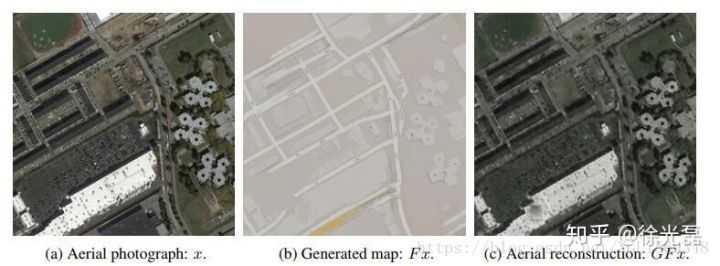
（PS：Cycle GAN这样的方法只能说大部分时候是work的，但是毛病也不少，举例NIPS2017的CycleGAN: a Master of Steganography指出Cycle GAN的做法，不能保证output图片中可用于重构input的信息是以原始方式保存的。

如下图的例子，白色的高亮建筑的特点并没有在output中呈现出来，但是$G_{Y->X}$的确完成了恢复重构input的工作。文章认为，这部分的信息被转写隐藏到了图片的其他位置中（Steganography）。

Star GAN

在之前的GAN中，每个G都只能完成一个特定domain到另一个特定domain的转换过程。Star GAN想要做的是，我们训练出来的G可以完成任意多个domain之间的互相转换。

在Star GAN中，我们的D的输入和往常一样，输出有两个，一个是判断$input$是否真实，另一个是判断input应该属于哪个domain。而我们的G接收两个输入，一个是$input$图片，另一个是目标domain，输入一个$output$图片，这张$output$图片除了将被扔入D来帮助D训练外，还将被再次扔入G，去生成一个原始domain的重构图片$input_{2}$，我们再通过比较$input$和$input_{2}$的差距来帮助训练G。（Loss式子的结构都和前文中模型类似，就不写了 ）

这里的domain可以是多种类型的独热编码的组合，以此可以表达出多种数据集中的多种特征，一个模型来实现多个生成效果的组合。

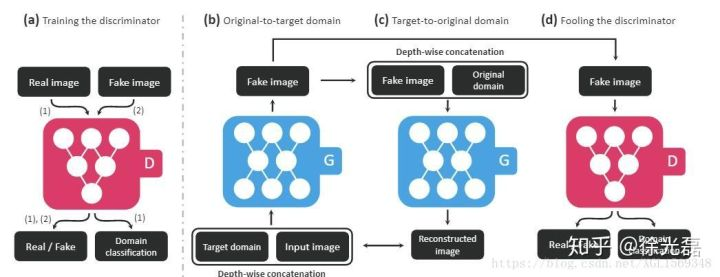
StarGAN: Unified Generative Adversarial Networks for Multi-Domain Image-to-Image Translation

CoGAN

CoGAN想要解决的问题，也是Unsupervised Conditional GAN。

如下图，假设我们拥有一个两套针对domain X与Y的自动编码机，我们希望的是，$Encoder_{X}$与$Encoder_{Y}$能够分别对domain X与Y进行正确的编码，输出的feature也要是同一体系的。假如我们把这两套自动编码机分开训练的话，显然我们不能保证中间橙色部分的feature是相同的表示，这样就会导致Decoder交叉工作时候发生错误。

为了解决这样的情况，我们需要把两个Encoder的末几个hidden layers需要共享参数，从而保证feature的正常表示，两个Decoder的前几层共享参数，从而保证feature的正常读取。

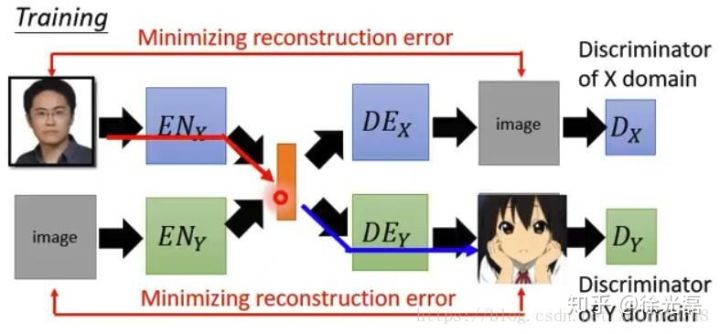
基于以上的想法，我们在Generator中的共享参数方式表示如下图。

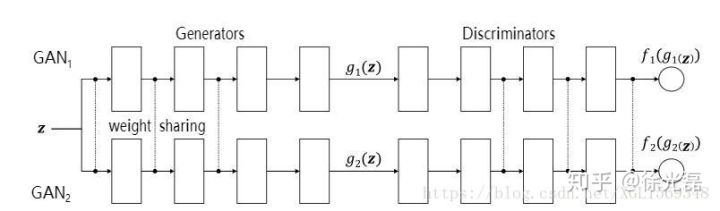Coupled Generative Adversarial Networks

(基于解决feature分布不同问题的还有很多种方法。例如，我们引入一个额外的$D_{domain}$来对中间的feature部分进行判断，看这个被encode出来的feature到底是哪个domain里的。如果$D_{domain}$能够判别出feature的domain信息，说明feature还是依赖了domain信息。我们的训练目标就是使两个domain的input经过encode后能够让$D_{domain}分不出是来自于哪个feature的，这就说明两种feature都是同一分布，也就解决了问题。)

Combo GAN

Combo GAN也是对应Unsupervised Conditional GAN问题。

前面我们提到了feature的分布可能不同的问题，Combo GAN的解决方式是，我们干脆让$input$经过$Encoder_{X}$，生成$feature_{X}$，再经过$Decoder_{Y}$生成一张$output_{Y}$图片，$output_{Y}$再作为$Encoder_{Y}$的输入再次输出一次$feature_{Y}$，最后经过$Decoder_{X}$生成$output_{X}$图片。通过结算$output_{X}$与$input$的距离来作为一个Cycle Loss。这个思路潜在的思维是，假如我们两个Decoder的输出feature分布是不同的话，那么在$Decoder_{Y}$这一步，图片就会被玩坏，自然就不能够重构出正确的$output_{X}$。

ComboGAN: Unrestrained Scalability for Image Domain Translation

（基于图片被玩坏这个猜想，显然$feature_{X}$和$feature_{Y}$的距离也不会小，这部分其实就是XGAN里提到的Sematic Consistency Loss。）

Patch GAN

GAN后来被实验认为面对大分辨率图像生成的任务中表现逊色，而Patch GAN的想法是让我们拥有多个D，分别观察大分辨率图像的各个局部图片（或语音上的局部），最后综合得到一个scalar。防止训练出来的D过拟合或是训练效率低。

这个判别器的设计思路被Cycle GAN等许多GAN采用。

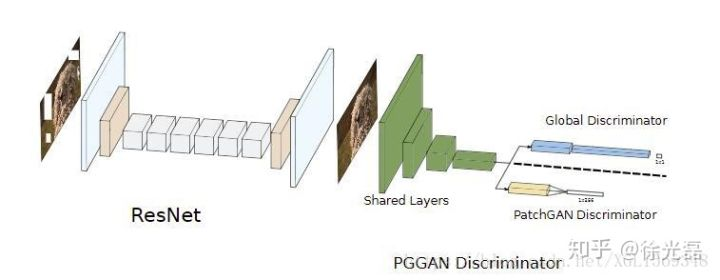Patch-Based Image Inpainting with Generative Adversarial Networks

Stack GAN

Stack GAN想解决的问题同样是大分辨率图像生成的任务。

它的想法是，在G的生成网络中，采用分级输出的方式，一个$G_{1}$输出6464的图片,$D_{1}$来进行评判，我们又拿来一个$G_{2}$把6464放大到256*256，再有$D_{2}$……通过级联的方式来保证最后大分辨率图像的输出质量。

训练的时候应先训练$G_{1}$，再训练$G_{1}$与$G_{2}$的级联，如此循环地进行“套娃”式地训练过程。

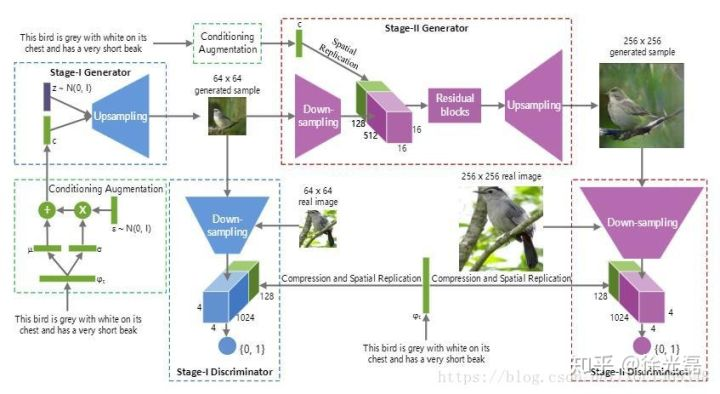StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks

Info GAN

对于所有生成模型来说，我们都希望知道input的vector每一个维度代表了什么样的语义，有什么具体的均匀的影响。我们均匀地变化某一维度的值时，我们期待output也是均匀地变化。

InfoGAN的思路是我们在输入的vector中加入多维的c作为一个编码，用来表示具体的语义，其他部分仍然是随机噪音。训练目标就是使得G能够准确输出一个和c有高度相关性的output，所以我们引入一个Classifier来判断output对应的c是什么。原文在目标函数中添加了一项$\lambda I(c;G(z,c))$，以mutual information（互信息）的方式来评判c与output之间的关系。 $I(c;G(z,c)) = H(c) - H(c;G(z,c))$ H是熵，衡量不确定度。

因为 $P(c|x)$ 不好得到，故原文使用变分分布$Q(c|x)$来逼近 $P(c|x)$ ，通过Variational Information Maximization的方式求出下界。

最后注意让Classifier和Discriminator前几层共享参数（他们的input同一分布）。

最后的效果

InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets

VAE-GAN

VAE-GAN是一个把VAE和GAN结合的产物。VAE和GAN同为生成模型，VAE的问题是生成的图片很容易过于模糊，不够realistic，GAN的问题是G不好训练。所以把两者结合起来，互相加强。

如下图中的架构，VAE-GAN相当于把GAN中的G换成了一个Autoencoder，或者说为VAE的output增加一个D来增强监督。

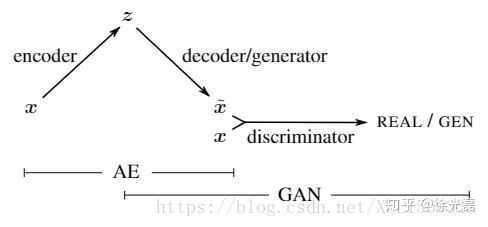
encoder的目标是使得z属于一个正态分布（通过KL散度），decoder的目标是欺骗D，AE的目标是降低reconstruction error，D的目标是区分出图片的真假。

Autoencoding beyond pixels using a learned similarity metric

BiGAN

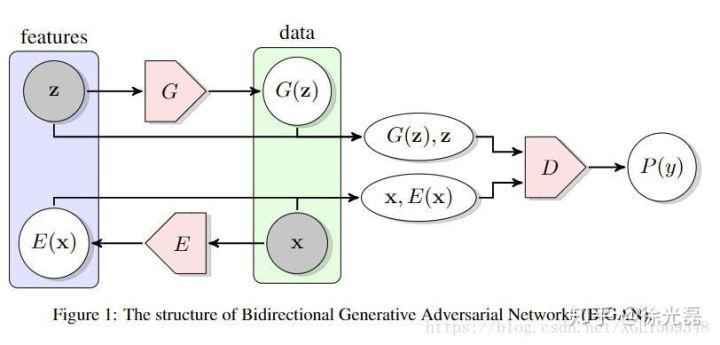
BiGAN应该说是一个利用GAN的思想来帮助训练VAE的模型。在BiGAN中，Encoder和Decoder不再是链接起来训练，而是通过一个Discriminator来监督各自训练。这个Discriminator接受code和image，输出的是输入数据的来源（encoder or decoder）。

设$x$取样real image，$x^{‘}$取样fake image，$z$取样正态分布，$z^{‘}$取样于把 $x$ encode的结果。 D的目的是提高$D(x,z^{‘})$，降低$D(x^{‘},z)$（其实反过来结果也是一样的）。 Encoder、Decoder的目的是提高$D(x^{‘},z)$，降低$D(x,z^{‘})$。

看上去Encoder和Decoder分开训练比较反直觉，但是实际上D还是在做衡量$P(x,z^{‘})$和$Q(x^{‘},z)$两分布差异的工作。

假如说不采用对抗的方式，我们尝试用z和x各自的reconstruction error来训练的话，其实目标是一模一样的，但是实际上这种思路训练出来的效果不如BiGAN。

Adversarial Feature Learning

Triple GAN

Triple GAN是利用了GAN的对抗思路，完成一个Semi-supervised的任务。首先，Triple GAN的目标是在绝大部分已有数据未打label的情况下训练出一个Classifier。

遮住Classifier先不看，G和D的主要工作思路和cGAN类似。加入的Classifier可以通过已打label的$(X_{l},Y_{l})$来学习，也可以通过G生成的$(X_{g},Y_{g})$来学习。同时Classifier为未打label标签进行分类后，这个$(X_{c},Y_{c})$会帮助D进行学习。

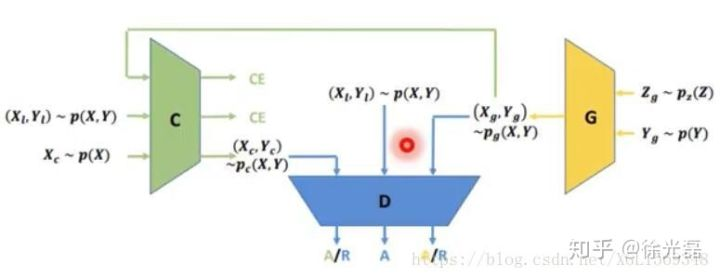
Triple Generative Adversarial Nets

本文的所有图片若无注明，均来自原始论文的截图或Hung-yi Lee的Tutorial for Generative Adversarial Network。